Довольно интересная конструкция, исследованная Милорадом Стевановичем. Все эти факты связанны с конструкцией инцентра треугольника BCI_A. Пока что я знаю только решения со счетом в синусах, однако предположу, что есть и без счета (особенно во второй, где эта точка является трилинейным полюсом прямой Монжа вписанных окружностей ABI, BCI, ACI)
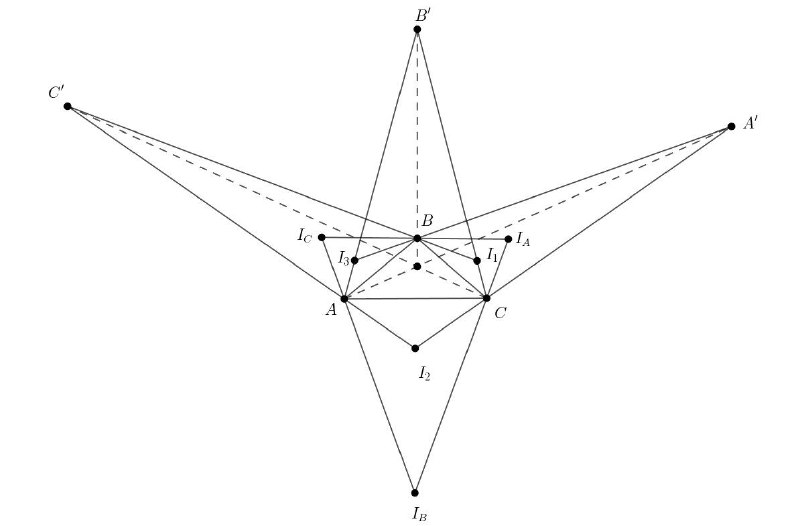
Дан треугольник ABC, точки I_A, I_B, I_C - эксцентры, I - инцентр. I_1 - инцентр BCI_A, I_2, I_3 определяются аналогично.
1. Пусть BI_1 и AI_2 пересекаются в точке C'. Аналогично определим A' и B' Докажите, что AA', BB', CC' пересекаются в 1 точке.
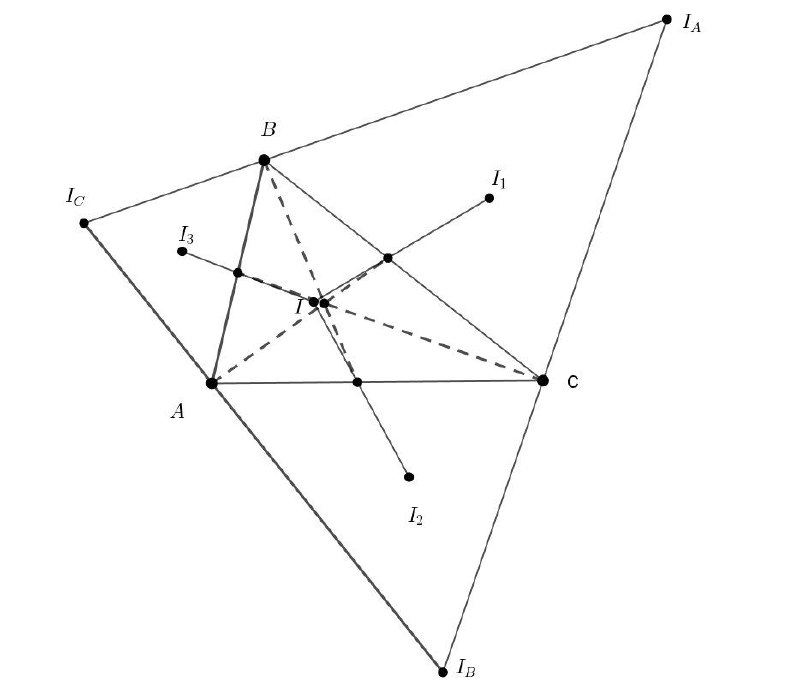
2. Пусть II_3 пересекает AB в точке C' определим A' и B' аналогично. Докажите, что AA',BB', CC' пересекаются в 1 точке.
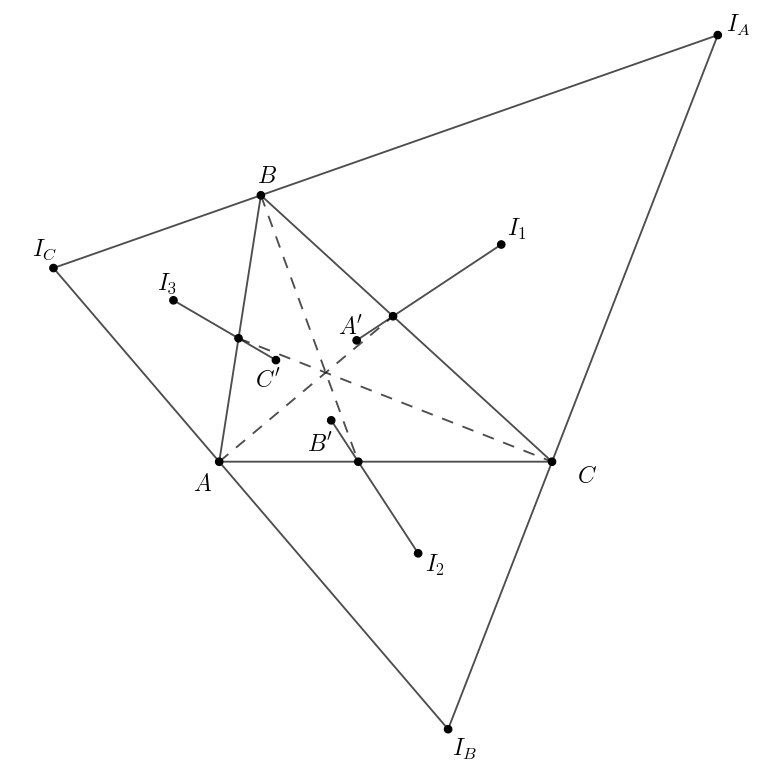
3. Пусть A', B', C' - инцентры BCI, ACI, ABI. I_1A' пересекает BC в точке A''. B'' и C'' определим аналогично. Докажите, что AA", BB'', CC'' пересекаются в 1 точке.
Дан треугольник ABC, точки I_A, I_B, I_C - эксцентры, I - инцентр. I_1 - инцентр BCI_A, I_2, I_3 определяются аналогично.
1. Пусть BI_1 и AI_2 пересекаются в точке C'. Аналогично определим A' и B' Докажите, что AA', BB', CC' пересекаются в 1 точке.
2. Пусть II_3 пересекает AB в точке C' определим A' и B' аналогично. Докажите, что AA',BB', CC' пересекаются в 1 точке.
3. Пусть A', B', C' - инцентры BCI, ACI, ABI. I_1A' пересекает BC в точке A''. B'' и C'' определим аналогично. Докажите, что AA", BB'', CC'' пересекаются в 1 точке.
👍3
tgoop.com/zadacha_dna/222
Create:
Last Update:
Last Update:
Довольно интересная конструкция, исследованная Милорадом Стевановичем. Все эти факты связанны с конструкцией инцентра треугольника BCI_A. Пока что я знаю только решения со счетом в синусах, однако предположу, что есть и без счета (особенно во второй, где эта точка является трилинейным полюсом прямой Монжа вписанных окружностей ABI, BCI, ACI)
Дан треугольник ABC, точки I_A, I_B, I_C - эксцентры, I - инцентр. I_1 - инцентр BCI_A, I_2, I_3 определяются аналогично.
1. Пусть BI_1 и AI_2 пересекаются в точке C'. Аналогично определим A' и B' Докажите, что AA', BB', CC' пересекаются в 1 точке.
2. Пусть II_3 пересекает AB в точке C' определим A' и B' аналогично. Докажите, что AA',BB', CC' пересекаются в 1 точке.
3. Пусть A', B', C' - инцентры BCI, ACI, ABI. I_1A' пересекает BC в точке A''. B'' и C'' определим аналогично. Докажите, что AA", BB'', CC'' пересекаются в 1 точке.
Дан треугольник ABC, точки I_A, I_B, I_C - эксцентры, I - инцентр. I_1 - инцентр BCI_A, I_2, I_3 определяются аналогично.
1. Пусть BI_1 и AI_2 пересекаются в точке C'. Аналогично определим A' и B' Докажите, что AA', BB', CC' пересекаются в 1 точке.
2. Пусть II_3 пересекает AB в точке C' определим A' и B' аналогично. Докажите, что AA',BB', CC' пересекаются в 1 точке.
3. Пусть A', B', C' - инцентры BCI, ACI, ABI. I_1A' пересекает BC в точке A''. B'' и C'' определим аналогично. Докажите, что AA", BB'', CC'' пересекаются в 1 точке.
BY Задача дня
Share with your friend now:
tgoop.com/zadacha_dna/222
