Акопян Геометрия в картинках 4.5.9

Сама задача довольно простая, но сама картинка очень глубокая. Покажу вот такое решение, которое я обнаружил сегодня.

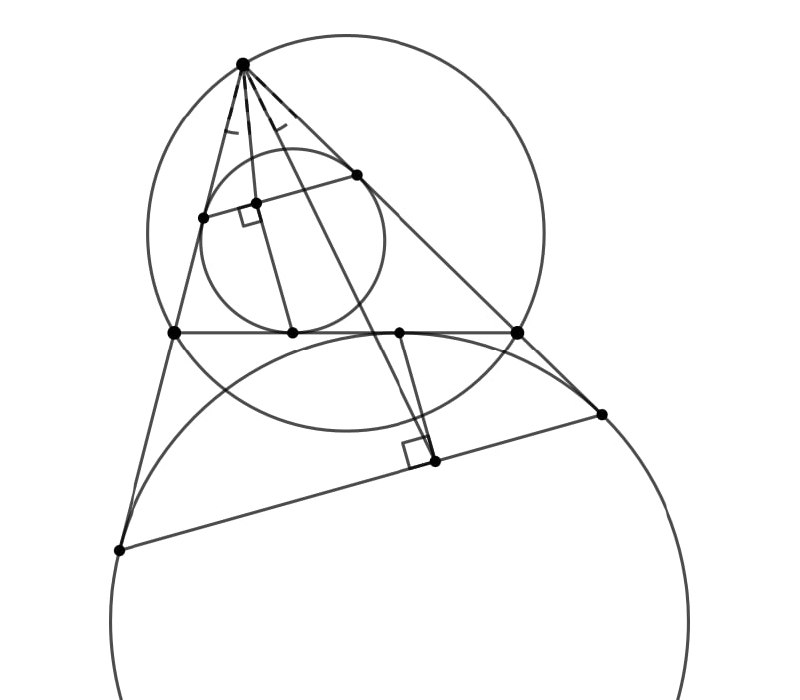
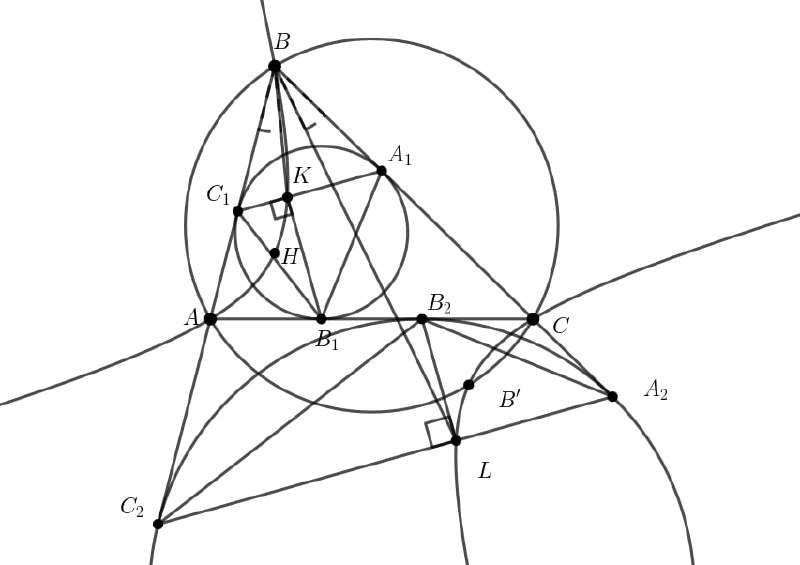
Итак проведем равнобокую гиперболу изогонально сопряженную серперу. Нам надо доказать, что K и L на изогоналях, тогда докажем, что существует проективная инволюция пучка из B меняющая следующие пары BK,BL; BH, BB' (где B' - диаметрально противоположна B); BA, BC. Спроецируем на гиперболу (благо точка B на ней лежит). Получим, что надо доказать проективную инволюцию меняющую A,C; K,L; H, B'. Но проективная инволюция коники - центральная проекция. Значит надо доказать, что KALC - параллелограмм. Но AK/KC=CL/LA, биссектрисы AKL и CLA (KB_1 и LB_2) параллельны (не сложный счет углов) С учетом расположения точек (K, L с разных сторон от AC) получаем, что при фиксированных ACK L восстанавливается единственным образом (пересечение прямой и окружности аполлония). Но точка симметричная K относительно середины подходит на роль L, значит это и есть L.