tgoop.com/the_algorithms/4597
Last Update:
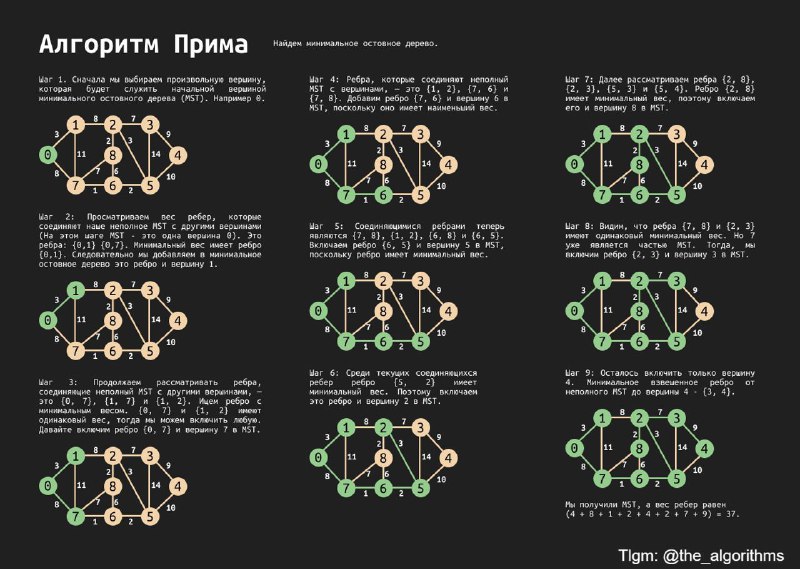
Алгоритм Прима
Алгоритм в теории графов для поиска минимального остовного дерева (MST) связного неориентированного графа с взвешенными ребрами.
Минимальное остовное дерево — это подграф, который включает все вершины исходного графа, образует дерево (без циклов) и имеет минимально возможную сумму весов ребер.
Алгоритм:
1. Начните с пустого набора, представляющего минимальное связующее дерево (MST). Выберите произвольную начальную вершину (обычно первую) и добавьте ее в MST.
2. Пока MST содержит менее V вершин: Определите ребро минимального веса, которое соединяет вершину в MST с вершиной вне MST и добавьте в MST вершину, соединенную выбранным ребром, вместе с самим ребром.
3. Продолжайте процесс выбора ребер, пока MST не будет содержать все вершины V.
4. Алгоритм завершен, когда MST содержит все вершины исходного графа.
Сложность: O(E + V log V)
BY Алгоритмы и структуры данных
Share with your friend now:
tgoop.com/the_algorithms/4597
