Математические байки
Nim-cube.pdf
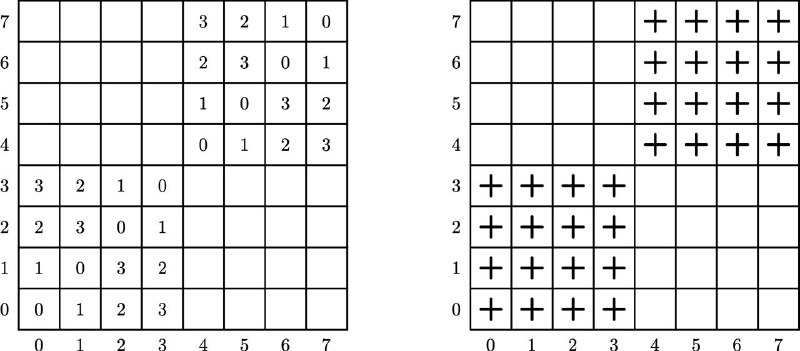
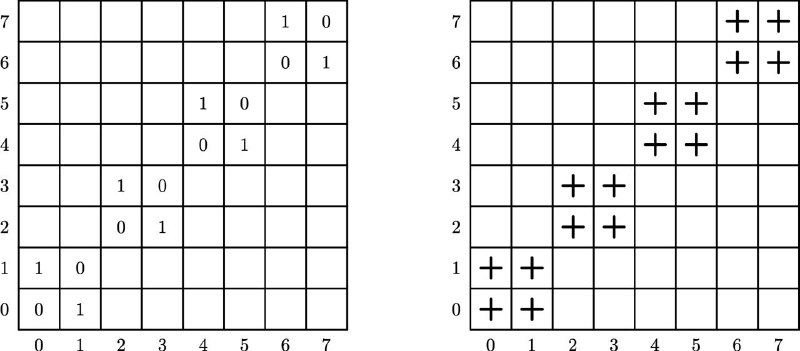
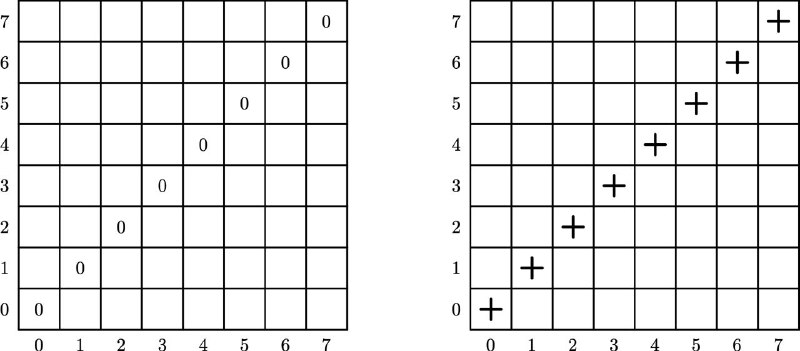
Если посмотреть на расположения проигрышных позиций, которые появляются на уровне k=0, на первых двух k=0,1 и на первых четырёх k=0,1,2,3 — то бросаются в глаза цепочки квадратов со стороной 1-2-4 соответственно, выстраивающихся вдоль главной диагонали.
И становится ясно, что так продолжается и дальше: если (уже в бесконечном октанте) посмотреть на первые 2^m уровней, когда в третьей кучке k=0,..., 2^m -1 камней, то проявившиеся проигрышные позиции заполняют цепочку квадратов со стороной 2^m. После чего на следующих 2^m уровнях точно так же заполняются квадраты над/под этой цепочкой, которые дополняют эту цепочку до цепочки вдвое больших квадратов.
И становится ясно, что так продолжается и дальше: если (уже в бесконечном октанте) посмотреть на первые 2^m уровней, когда в третьей кучке k=0,..., 2^m -1 камней, то проявившиеся проигрышные позиции заполняют цепочку квадратов со стороной 2^m. После чего на следующих 2^m уровнях точно так же заполняются квадраты над/под этой цепочкой, которые дополняют эту цепочку до цепочки вдвое больших квадратов.
tgoop.com/mathtabletalks/4369
Create:
Last Update:
Last Update:
Если посмотреть на расположения проигрышных позиций, которые появляются на уровне k=0, на первых двух k=0,1 и на первых четырёх k=0,1,2,3 — то бросаются в глаза цепочки квадратов со стороной 1-2-4 соответственно, выстраивающихся вдоль главной диагонали.
И становится ясно, что так продолжается и дальше: если (уже в бесконечном октанте) посмотреть на первые 2^m уровней, когда в третьей кучке k=0,..., 2^m -1 камней, то проявившиеся проигрышные позиции заполняют цепочку квадратов со стороной 2^m. После чего на следующих 2^m уровнях точно так же заполняются квадраты над/под этой цепочкой, которые дополняют эту цепочку до цепочки вдвое больших квадратов.
И становится ясно, что так продолжается и дальше: если (уже в бесконечном октанте) посмотреть на первые 2^m уровней, когда в третьей кучке k=0,..., 2^m -1 камней, то проявившиеся проигрышные позиции заполняют цепочку квадратов со стороной 2^m. После чего на следующих 2^m уровнях точно так же заполняются квадраты над/под этой цепочкой, которые дополняют эту цепочку до цепочки вдвое больших квадратов.
BY Математические байки
Share with your friend now:
tgoop.com/mathtabletalks/4369
