Идея атаки очень простая. Для более простого теоретического примера представим, что нам дано API, которое возвращает логиты для следующего токена по префиксу. Вспомним, что последний слой в LLM (как минимум, в рассматриваемом случае) – это матрица W (h × l), которая проецирует активации предпоследнего слоя размерностью h в вектор размерности l, где l – это размер словаря (|V|). Сгенерируем n случайных префиксов и отправим их в языковую модель, получив логиты для следующего токена и сложим их в матрицу Q размерностью n × l.

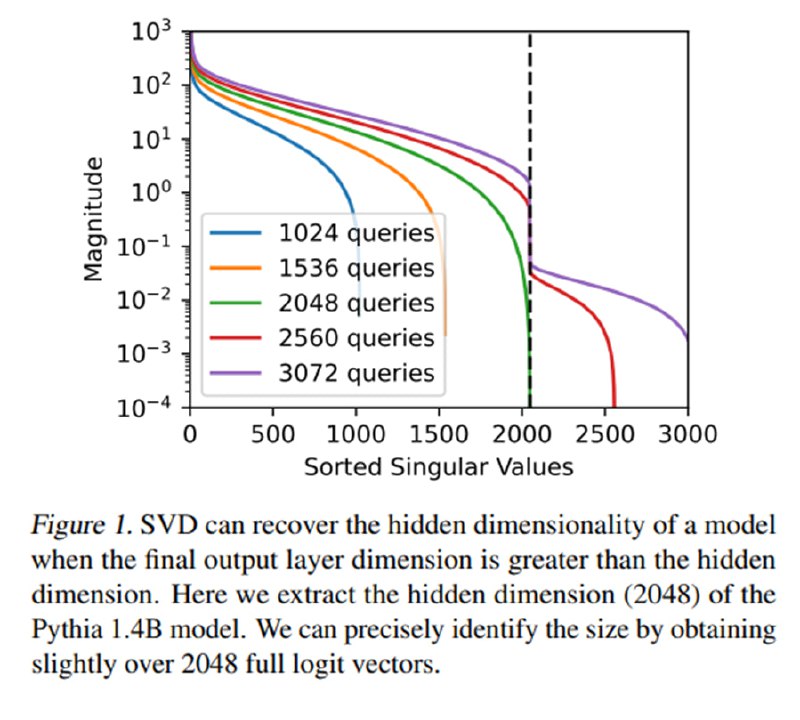
Учитывая отсутствие нелинейностей, можно заключить, что вектора, составляющие матрицу Q, на самом деле лежат не в пространстве размерности l, а в его подпространстве размерности h. Теперь вспомним, что есть такая штука, как сингулярное разложение, которая позволяет нам решать задачу приближения матрицы матрицей меньшего ранга. При разложении мы получаем три матрицы (U, Σ, V*), где матрица Σ – это диагональная матрица с упорядоченными по убыванию сингулярными числами на главной диагонали. Если эффективная размерность раскладываемой матрицы размерностью l на самом деле h, то сингулярные числа начиная с h будут равны нулю (в реальности из-за численных особенностей вычислений они будут близки к нулю).

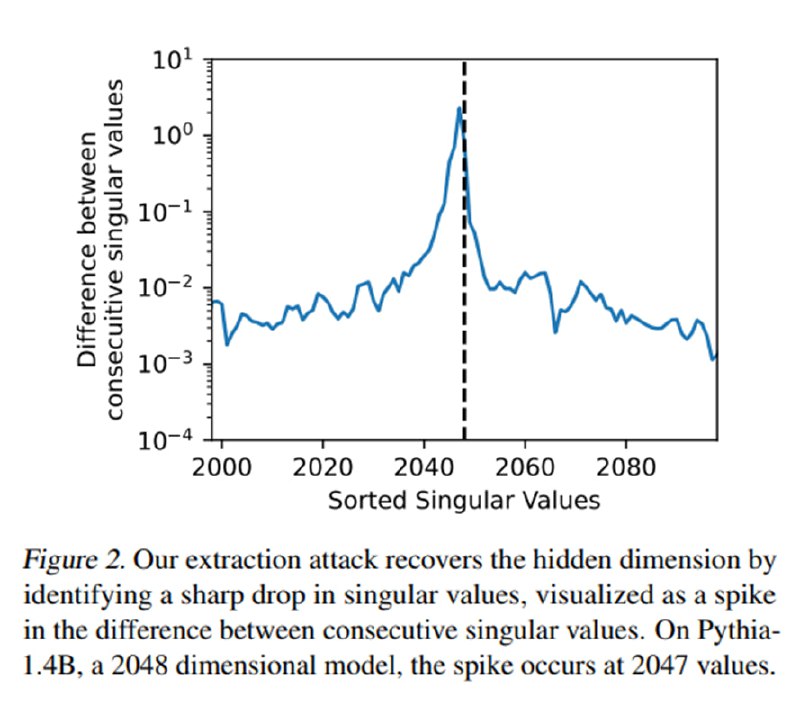
Исходя из этого, мы получаем следующий алгоритм: посчитаем SVD от матрицы Q и посмотрим, на каком индексе получается максимальное падение сингулярного числа относительно предыдущего – это и будет искомая размерность h, что авторы демонстрируют на наборе open-source-моделей с известной размерностью матриц весов.

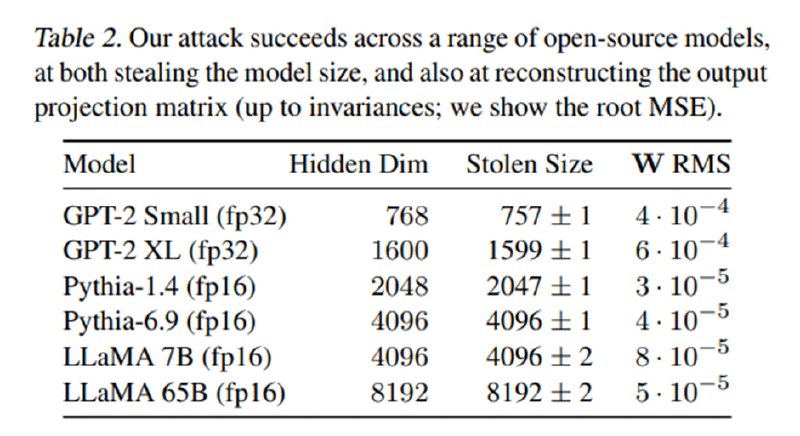
Осталось достать веса. Авторы доказывают, что U · Σ = W · G, где первые две матрицы нам известны после SVD, а W – искомая матрица весов последнего слоя с точностью до аффинного преобразования G. Для доказательства этого они находят матрицу G и демонстрируют, что разница между реальной матрицей и W · G минимальна.