tgoop.com/bminaiev_blog/22
Last Update:
Площадь многоугольника
Недавно вычислял площадь выпуклого многоугольника. Для этого существует очень простой алгоритм. Нужно по всем ребрам просуммировать их "ориентированную площадь".
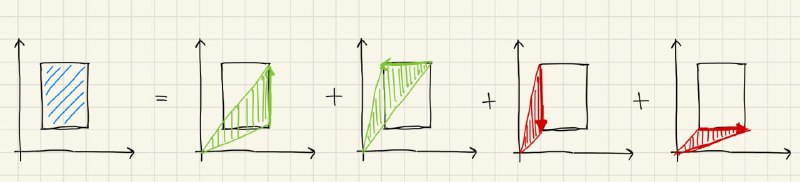
Есть разные варианты того, что считать "ориентированной площадью". Например, можно считать площадь треугольника, у которого одна из вершин точка (0, 0), а две других — концы ребра. В зависимости от того, какая вершина видна под меньшим углом из начала координат, площадь нужно взять с плюсом или с минусом.
Получается простой код:fn area(pts: &[Point]) -> f32 {Этот способ называют формулой Гаусса.
let mut res = 0.0;
for i in 0..pts.len() {
let p1 = pts[i];
let p2 = pts[(i + 1) % pts.len()];
res += p1.x * p2.y - p1.y * p2.x;
}
res.abs() / 2.0
}
Иногда используют площади трапеций, но суть от этого не меняется.
Но не все так просто! Вчера я написал этот алгоритм, посчитал площадь квадрата 1х1 и получил 0.0. Проблема была в том, что хоть квадрат и был маленьким, его координаты были порядка нескольких тысяч и хранились в f32. Казалось бы у типа f32 есть 23 бита мантиссы и их должно хватать, чтобы сохранить число порядка нескольких тысяч. Но на самом деле проблема в том, что при вычислении векторного произведения нужно перемножить два числа порядка нескольких тысяч (результат уже нельзя абсолютно точно сохранить в f32), а потом вычесть такое же по порядку число. От этого накапливается погрешность, и получается 0.0 в результате.
Как исправить алгоритм? Довольно хорошо работающий способ — вместо точки (0, 0) взять первую точку многоугольника, и все векторные произведения считать от нее:fn area(pts: &[Point]) -> f32 {Но такой трюк не всегда решает проблему (например, в случае с невыпуклыми многоугольниками). Так что по возможности лучше просто избегать чисел с плавающей точкой :)
let mut res = 0.0;
for i in 0..pts.len() {
let p1 = pts[i] - pts[0];
let p2 = pts[(i + 1) % pts.len()] - pts[0];
res += p1.x * p2.y - p1.y * p2.x;
}
res.abs() / 2.0
}
BY Боря программирует
Share with your friend now:
tgoop.com/bminaiev_blog/22
