Возвращаемся к а), часть-2, товарищи статистики!
- вероятность (перевзвешанная) альтернативной гипотезы через значение p-value,
Это часть будет сложнее, она и у меня собирается по частям так-то, так что жуйте без спешки.
Напомню: число успешных тестов, Success Rate, не очень велико, как и говорил, это 5-10%, зависит от индустрии -> можете посмотреть эти данные от Microsoft, Neflix и пр.
б) Возьмём, что в нашем случае оно составляет 10%. И пускай при этом все из них были действительно успешны, true positive. Значит, шансы, что наша конкретная гипотеза в конкретном эксперименте будет успешна P(HA) = 10% = 0.1
Распишем согласно Баейсу (пост с разбором формулы тут) вероятность P(HA|p-value) как переоценка HA при условии "конкретного" p-value:
P(HA|p-value) = P(p-value|HA)*P(HA)/P(p-value)
P(p-value|HA) - вероятность конкретного p-value при верности HA
P(HA) - вероятность HA = 0.1
P(p-value) - вероятность конкретного значения p-value
P(p-value) = P(p-value|HA)*P(HA)+P(p-value|-HA)*P(-HA)
или
P(p-value|HA)*P(HA)+P(p-value|H0)*P(H0)
P(H0) = 1 - P(HA) = 0.9
Нам нужно выяснить, чему равно P(p-value|HA), P(p-value|H0)
Сделаем это.
Предварительно мы сделали дизайн теста, альфа = 0.05, мощность = 0.8, выяснили MDE.
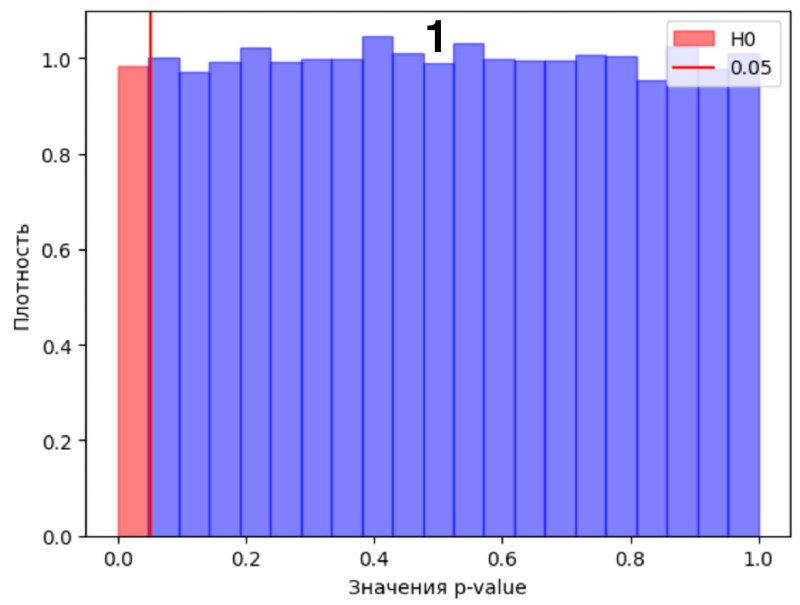
1) Далее сделали симуляцию распределений p-value когда эффекта нет (верна H0), p-value ожидаемо в 5% случае оказался от 0.05 и ниже согласно альфе, см. картинку 1
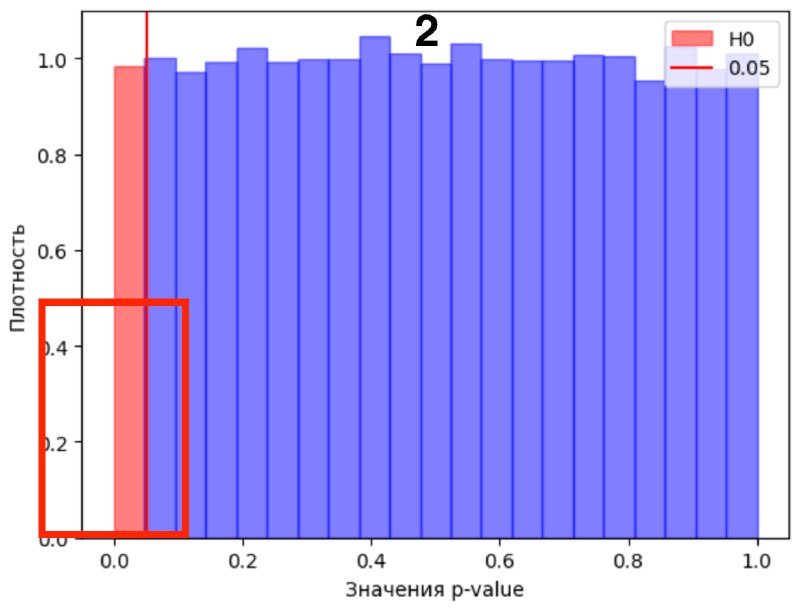
При этом важно (!) cтат. значимый результат при H0 может быть в обе стороны у нас, нас интересует только ложноположительность, когда результат для нас положительный. А это случается в половине всех p-value <= alpha. То есть от красного квадратика мы берем половину, картинка 2!
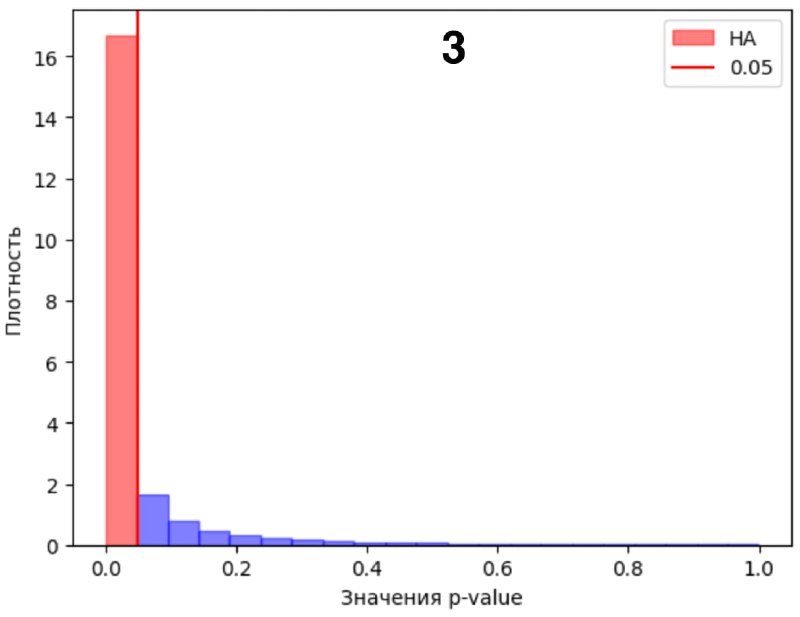
2) Далее подсчитали, когда эффект есть (HA), p-value ниже 0.05 в 80% согласно мощности, картинка 3.
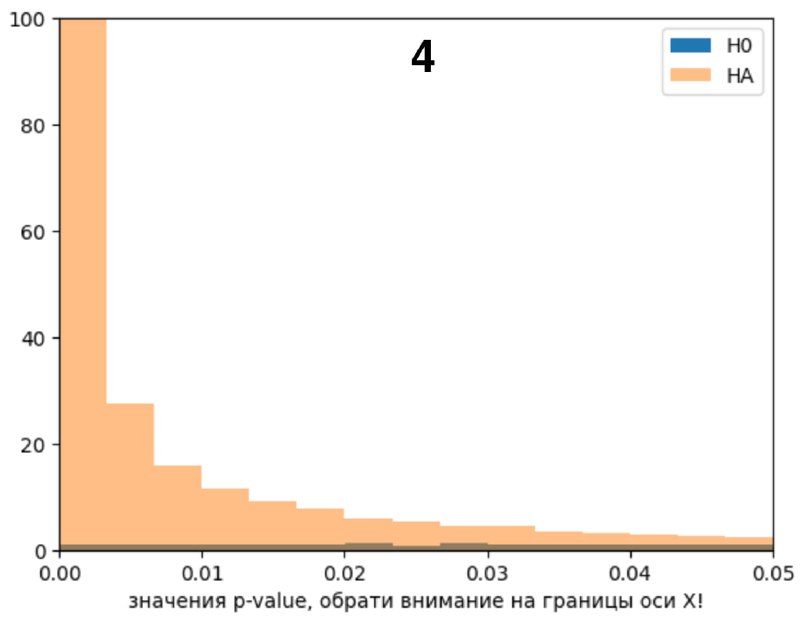
3) Посмотрим только те p-value по H0 и HA, которые <= 0.05, то есть стат. значимые согласно альфе, картинка 4
Продолжение ниже...
- вероятность (перевзвешанная) альтернативной гипотезы через значение p-value,
Это часть будет сложнее, она и у меня собирается по частям так-то, так что жуйте без спешки.
Напомню: число успешных тестов, Success Rate, не очень велико, как и говорил, это 5-10%, зависит от индустрии -> можете посмотреть эти данные от Microsoft, Neflix и пр.
б) Возьмём, что в нашем случае оно составляет 10%. И пускай при этом все из них были действительно успешны, true positive. Значит, шансы, что наша конкретная гипотеза в конкретном эксперименте будет успешна P(HA) = 10% = 0.1
Распишем согласно Баейсу (пост с разбором формулы тут) вероятность P(HA|p-value) как переоценка HA при условии "конкретного" p-value:
P(HA|p-value) = P(p-value|HA)*P(HA)/P(p-value)
P(p-value|HA) - вероятность конкретного p-value при верности HA
P(HA) - вероятность HA = 0.1
P(p-value) - вероятность конкретного значения p-value
P(p-value) = P(p-value|HA)*P(HA)+P(p-value|-HA)*P(-HA)
или
P(p-value|HA)*P(HA)+P(p-value|H0)*P(H0)
P(H0) = 1 - P(HA) = 0.9
Нам нужно выяснить, чему равно P(p-value|HA), P(p-value|H0)
Сделаем это.
Предварительно мы сделали дизайн теста, альфа = 0.05, мощность = 0.8, выяснили MDE.
1) Далее сделали симуляцию распределений p-value когда эффекта нет (верна H0), p-value ожидаемо в 5% случае оказался от 0.05 и ниже согласно альфе, см. картинку 1
При этом важно (!) cтат. значимый результат при H0 может быть в обе стороны у нас, нас интересует только ложноположительность, когда результат для нас положительный. А это случается в половине всех p-value <= alpha. То есть от красного квадратика мы берем половину, картинка 2!
2) Далее подсчитали, когда эффект есть (HA), p-value ниже 0.05 в 80% согласно мощности, картинка 3.
3) Посмотрим только те p-value по H0 и HA, которые <= 0.05, то есть стат. значимые согласно альфе, картинка 4
Продолжение ниже...
tgoop.com/abba_testing/36
Create:
Last Update:
Last Update:
Возвращаемся к а), часть-2, товарищи статистики!
- вероятность (перевзвешанная) альтернативной гипотезы через значение p-value,
Это часть будет сложнее, она и у меня собирается по частям так-то, так что жуйте без спешки.
Напомню: число успешных тестов, Success Rate, не очень велико, как и говорил, это 5-10%, зависит от индустрии -> можете посмотреть эти данные от Microsoft, Neflix и пр.
б) Возьмём, что в нашем случае оно составляет 10%. И пускай при этом все из них были действительно успешны, true positive. Значит, шансы, что наша конкретная гипотеза в конкретном эксперименте будет успешна P(HA) = 10% = 0.1
Распишем согласно Баейсу (пост с разбором формулы тут) вероятность P(HA|p-value) как переоценка HA при условии "конкретного" p-value:
P(HA|p-value) = P(p-value|HA)*P(HA)/P(p-value)
P(p-value|HA) - вероятность конкретного p-value при верности HA
P(HA) - вероятность HA = 0.1
P(p-value) - вероятность конкретного значения p-value
P(p-value) = P(p-value|HA)*P(HA)+P(p-value|-HA)*P(-HA)
или
P(p-value|HA)*P(HA)+P(p-value|H0)*P(H0)
P(H0) = 1 - P(HA) = 0.9
Нам нужно выяснить, чему равно P(p-value|HA), P(p-value|H0)
Сделаем это.
Предварительно мы сделали дизайн теста, альфа = 0.05, мощность = 0.8, выяснили MDE.
1) Далее сделали симуляцию распределений p-value когда эффекта нет (верна H0), p-value ожидаемо в 5% случае оказался от 0.05 и ниже согласно альфе, см. картинку 1
При этом важно (!) cтат. значимый результат при H0 может быть в обе стороны у нас, нас интересует только ложноположительность, когда результат для нас положительный. А это случается в половине всех p-value <= alpha. То есть от красного квадратика мы берем половину, картинка 2!
2) Далее подсчитали, когда эффект есть (HA), p-value ниже 0.05 в 80% согласно мощности, картинка 3.
3) Посмотрим только те p-value по H0 и HA, которые <= 0.05, то есть стат. значимые согласно альфе, картинка 4
Продолжение ниже...
- вероятность (перевзвешанная) альтернативной гипотезы через значение p-value,
Это часть будет сложнее, она и у меня собирается по частям так-то, так что жуйте без спешки.
Напомню: число успешных тестов, Success Rate, не очень велико, как и говорил, это 5-10%, зависит от индустрии -> можете посмотреть эти данные от Microsoft, Neflix и пр.
б) Возьмём, что в нашем случае оно составляет 10%. И пускай при этом все из них были действительно успешны, true positive. Значит, шансы, что наша конкретная гипотеза в конкретном эксперименте будет успешна P(HA) = 10% = 0.1
Распишем согласно Баейсу (пост с разбором формулы тут) вероятность P(HA|p-value) как переоценка HA при условии "конкретного" p-value:
P(HA|p-value) = P(p-value|HA)*P(HA)/P(p-value)
P(p-value|HA) - вероятность конкретного p-value при верности HA
P(HA) - вероятность HA = 0.1
P(p-value) - вероятность конкретного значения p-value
P(p-value) = P(p-value|HA)*P(HA)+P(p-value|-HA)*P(-HA)
или
P(p-value|HA)*P(HA)+P(p-value|H0)*P(H0)
P(H0) = 1 - P(HA) = 0.9
Нам нужно выяснить, чему равно P(p-value|HA), P(p-value|H0)
Сделаем это.
Предварительно мы сделали дизайн теста, альфа = 0.05, мощность = 0.8, выяснили MDE.
1) Далее сделали симуляцию распределений p-value когда эффекта нет (верна H0), p-value ожидаемо в 5% случае оказался от 0.05 и ниже согласно альфе, см. картинку 1
При этом важно (!) cтат. значимый результат при H0 может быть в обе стороны у нас, нас интересует только ложноположительность, когда результат для нас положительный. А это случается в половине всех p-value <= alpha. То есть от красного квадратика мы берем половину, картинка 2!
2) Далее подсчитали, когда эффект есть (HA), p-value ниже 0.05 в 80% согласно мощности, картинка 3.
3) Посмотрим только те p-value по H0 и HA, которые <= 0.05, то есть стат. значимые согласно альфе, картинка 4
Продолжение ниже...
BY Не AБы какие тесты
Share with your friend now:
tgoop.com/abba_testing/36