Под постом про оптимизацию несколько раз спросили про байесовские методы. Раньше они у меня не заводились, но мыжтутучёные, штош, придётся пробовать. 🤓

В качестве задачи я взял свой код для оптимизации цветовых палитр. Задача без тренировки дорогих сеток, но с большим количеством локальных минимумов и противной симметрией. Сравнил три популярных оптимайзера из Nevergrad с тремя из Оптуны, включая дефолтный TPE.

Результаты получились плохими для TPE, который оказался лишь капельку лучше случайного поиска. 📉

Популяционные алгоритмы типа CMA оказались сильно лучше, да еще и сильно быстрее – примерно в 10 раз из-за того, что никакой умной оценки параметров не производится . Реализация из Nevergrad оказалась в ~1.5 раза быстрее своего аналога из оптуны.

Есть такой фольклорный фактоид про задачу о разборчивой невесте (в англоязычной литературе её чуть более корректно называют "задачей о секретаре”) в теории оптимального выбора.

Задача даётся в подобной формулировке: дано N элементов (женихов), которые образуют строгий линейный порядок – каждая пара женихов сравнима, и нет ничьих. Женихи приходят в случайном порядке, при этом каждое решение окончательное (какой жених захочет пробовать второй раз, правда же? 💁‍♂️). Нужно разработать алгоритм, чтобы из этого потока выбрать лучшего жениха.

В такой формулировке оптимальная стратегия –
отвергнуть первые 1/ε≈36.8% женихов, а потом – выбрать первого, кто будет лучше всех предыдущих. Этот алгоритм особенно прочно закрепился в self-help книжках от Algorithms to live by до How not to die alone, которые пропагандируют его как универсальную эвристику для решения жизненных задач, и, конечно, поиска партнёра на жизнь. 🥵

Проблема в применении таких эвристик к реальной жизни, конечно, в деталях. В классической формулировке мы сфокусированы на поиске лучшего кандидата, и нас абсолютно не устраивает никакой другой 💔. Можно представить чуть более мягкую и реалистичную версию, когда наша награда за кандидатов распределена равномерно от 0 до 1. Тогда оптимальное время перейти к поиску уменьшается с N/ε до аж √N, что существенно раньше, чем в классической версии.

У проблемы секретаря существует ещё много интересных вариаций, которые до сих пор (!) остаются нерешёнными. Например, моей коллега в 2020 году вывел алгоритм для игры с практически любыми распределениями ценностей женихов, где вероятность выигрыша составляет 51.7%.

Выбирайте с умом! 💡

Как оценить вероятность событий, которые никогда не происходили?

Вчера Caltrain (электричка для бомжей жителей кремниевой долины) насмерть сбил двух человек в двух независимых инцидентах. За полгода от рук поездов погибло уже 4 человека. В это же время в кремниевой долине – дивный новый мир с самоуправляемыми повозками набирает обороты 🦆. За январь и февраль этого года полностью автономные машины Cruise и Waymo никого не сбили насмерть (из тех, о ком нам рассказали🪖). Можем ли мы как-то сравнить вероятность гибели от электричек и автономных автомобилей?

Можем! Для этого нам понадобится аддитивное сглаживание, которое по-выпендрёжному называется сгаживанием Лапласа. В далёком 1814 Лаплас вывел эту чудную формулу для того, чтобы оценить, взойдёт ли завтра солнце (спойлер для тру-байесовцев – взойдёт). У аддитивного сглаживания есть несколько вариантов, но я сегодня расскажу про самый простой, но такой же эффективный.😛

Обозначим количество наблюдений как n и произошедших событий как nₛ. Наша оценка пропорции с аддитивным сглаживанием будет равна (nₛ+1)/(n+1). Просто добавь адын. 🥛

Для нашей задачки про смерть я нашёл такие данные:
1. Caltrain возит ~60000 пассажиров в день, средняя поездка – 40км. Получаем 60000*40=2.4 миллиона пассажиро-километра в день.
2. Cruise с Waymo в конце февраля накатали 11 миллионов километров. Предположим, что в среднем в машине было 1.5 человека и получим 1.5*11/55=0.3 миллиона пассажиро-километра в день.

Подставляем цифры в формулу и получаем (4+1)/2.4 = 2.08 ожидаемых смерти на миллион пассажиро-километров для поездов и (0+1)/0.3 = 3.33 ожидаемых смерти на миллион пассажиро-километров для робо-машин. Так что с общественного транспорта пока слезать стимула нет. 🎒

Хочу рассказать небольшую историю про эпиграф своей кандидатской диссертации: "η δε γνώσις αγάπη γίνεται" из "О душе и воскресении" Григория Нисского. Переводится на русский это примерно как "познание становится любовью". 🤓

Эпиграф – это отличное место, чтобы контекстуализировать свой жизненный опыт (читай: повыпендриваться, потому что никто в здравом уме диссертации не читает). Эту цитату без определённого артикля η использовал Павел Флоренский как эпиграф к своей монографии "Столп и утверждение истины". Однако, без него фраза радикально меняет своё значение на "познание порождается любовью", которое и используется до сих пор как перевод даже в гороскопах.

Продолжаем тур по достойным внимания книгам.

Сегодня у нас на очереди обзорная книга Ави Видгерзона, который в 2021 году вместе с Ласло Ловасем удостоился Абелевской премии за “фундаментальный вклад в теоретическую информатику и дискретную математику, а также за ведущую роль в их становлении как центральных направлений современной математики”.

Книжка называется Mathematics and Computation и доступна для скачивания с сайта автора. Как можно догадаться по названию, рассказывает про теорию алгоритмов (theory of computation) в формате “галопом по Европам”🦆. Вот только вместо привычного лёгкого научпопа нас ждёт очень плотное ревью по темам от достаточно стандартных – вычислительная сложность, случайность, сложность доказательств – до квантовых вычислений, криптографии, распределённых вычислений, и, конечно, нашего любимого машинлёрнинга. 👥

Про “плотность ревью” я не шучу – вместе с историческими справками по областям часто упоминаются последние значительные достижения с обильными цитатами, так что при желании на каждой странице можно зависнуть на денёк-другой 🤓. Но при этом книга написала так живо, что, если не задумываться, можно читать её почти как своеобразный математический нон-фикшн.

Хочу научиться так писать. 😟

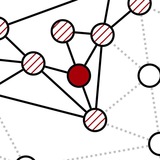
Американское патентное бюро решило не сильно отставать от академиков из JMLR, и выпустило нашу патентную заявку, которую мы подали в сентябре 2020 года. 🐌

Патент по сути повторяет нашу статью про ультра-быстрые распределённые эмбеддинги вершин в очень больших графах. В академии она не сильно понравилась: с разных конференций и журналов её реджектили аж 7 раз, зато две разных статьи “по мотивам”, которые по сути ничего не добавляют, взяли на KDD. 💥

Один из плюсов работы в индустрии – это, что не обязательно получать мужское одобрение рецензентов, достаточно проверить, что всё хорошо работает в проде. ☕️

Тайм-менеджмент

В конце прошлого года я наконец переехал в одну тайм-зону к большинству коллег. Это значит, что вместо того, чтобы полагаться на разницу во времени для того, чтобы не иметь слишком много встреч и совещаний, мне пришлось учиться тайм-менеджменту самому. Мне всё ещё кажется, что получается не очень оптимально, но время для работы почти всегда есть, а это уже большой прогресс.

Я классифицирую все блоки времени в календаре на личные встречи (1:1s), встречи по рисерчу и разработке (research & development) и встречи с клиентами (clients) – внутренними командами, которым мы помогаем использовать результаты нашего рисёрча. В категорию “другое” часто улетает пара часов в неделю, но что уж тут поделаешь. 💁‍♂️

Вроде, получилось неплохо. В среднем в неделе остаётся чуть больше 25 часов на собственно говоря работу. По крайней мере, понятно, что я занимаюсь рисёрчем фуллтайм, правда не очень коллаборативно. 📃

Про рецензии

Пару лет назад я где-то вычитал (не смог сейчас найти источник 🤷‍♂️) про две стратегии рецензирования научных статей. Мне кажется, что такой взгляд на рецензирование довольно ценный – несмотря на то, что я никогда не тратил много времени на ревью, меня выбирали как топ-рецензента на нипсе. ✨

Первая стратегия – nitpicker 🗡 – это для каждой статьи пытаемся найти её слабые стороны, и, если их набирается много, реджектим. Слабая теория? Минус пять баллов Гриффиндору. Мало экспериментов? Реджект. Много экспериментов? Не поверите, тоже реджект. 😈

Вторая – space curation 🧐 – в каждой рецензии мы думаем в совокупности о том, будет ли лучше от того, что эта конкретная статья появится на этой конкретной конференции. В этой стратегии нет совсем непростительных грехов – если общий результат очень полезный и интересный, можно и простить отсутствие какой-то новизны или слабую теорию – потом другие люди подхватят, и наоборот – качественно выполненные статьи с не очень интересными результатами могут вдохновить кого-то на интересную статью-продолжение. Но для того, чтобы это случилось, статья должна выйти – значит, нужно её принять. 💡

Ответом ко вчерашней загадке был вероятностный алгоритм – и уж извините за то, что не втиснул в условие, что решение должно быть почти достоверным. 💁‍♂️

Почти достоверность позволяет нам ценой редких ошибок на порядки снижать сложность разных алгоритмов. Собственно, из подобных алгоритмов и пошло название канала epsilon correct, хотя правильнее, конечно, было бы назваться 1-ε correct. Но как мы можем из "хоть сколько-нибудь" достоверного алгоритма сделать почти достоверный? 👀

Допустим, нам дан алгоритм A с выходами A(x)∊R. Например, A(x)∊{0,1} – x сортированный или нет. И если A выдаёт правильный ответ с вероятностью δ=51%, мы хотим эту веростность довести до (1-ε). Оказывается, этого можно достичь, если мы (независимо) выполним наш алгоритм O(log(1/ε)) раз и возьмём медианный результат. Доказательство можно посмотреть вот тут.

В случае бинарных исходов, для конкретных значений вероятности δ и ошибки ε результат медианного алгоритма следует биномиальному распределению, так что можно посчитать количество требуемых попыток точно. 👌

Стажировки

Сейчас разгар сезона стажировок – только сегодня я пообщался с тремя стажёрами, которые делают свои проекты при моём участии. И это ещё не вышла девушка, которой буду руководить непоследственно я. Быстрый способ почувстсвовать себя старым. 👴

Я сам был стажёром дважды – первый раз раз в 2019 году, в инженерной команде, которая делала горизонтальную систему анти-абьюз для разных систем гугла. Это было в Саннивейле в Калифорнии – тогда я точно понял, что там жить не очень хочется. Я тогда написал только одну статью, зато вфигачил много кода и экспериментов, так что в итоге получился длинный и красивый отчёт.

Второй раз я уже пошёл непосредственно в команду graph mining, в которой в итоге и остался. Дело было в феврале 2020 года в Нью-Йорке, и в офис я успел отходить примерно недели две 😭. Из-за ковида стажировку пришлось продлить – зато я успел написать две статьи, и тот самый патент, который опубликовали только недавно.

У меня несколько раз спрашивали, что является хорошим результатом для исследовательской стажировки (research internship, PhD level):
1. Подготовка одной полноценной статьи на конференцию уровня NeurIPS/ICLR/ICML.
2. Написание 4+ пулл-реквестов средней сложности – нет, исправить опчеатки не считается. Хорошо, когда интерн может написать свой алгоритм в наши фреймворки, но можно и наговнокодить мимо.
3. Запустить свой алгоритм на внутренних данных и нарисовать красивую картиночку. Умение рисовать красивые картиночки – недооценённый талант, который сильно помогает людям запоминать вашу работу.

Готово, вы великолепны!🤴

Мне говорили, что это много, но я регулярно вижу, что в команде этого достигают почти все стажёры, что до нас доходят. Посмотрим, что выйдет продуктивного из этого сезона стажировок.😑

Поехал на ICML – вторую по размеру конференцию по машинному обучению. Мы там покажем туториал по нашей библиотеке TensorFlow-GNN и пару воркшопных статей. Постер к моей любимой – на фото (ковёр для антуража 🇷🇺).

В этом году конференция на Гавайях, поэтому пропускать такое нельзя. 🏄‍♂️